Graph Traversal and Layout on a Cartesian Coordinate System
This is an overview of how to lay out a graph when your edges represent a cardinal direction.
Problem Overview
I have been working on a new MUD code base in Go. MUDs are a text only game played via telnet and other terminal oriented clients. One of the primary data structures in a MUD is the Room. Rooms are generally the place where everything happens in a MUD. They describe a general purpose area in the game world. Each room is connected to other rooms by cardinal directions. These connections in MUD nomenclature are called exits. In computer science they would be graph edges. It is convenient for many reasons to visualize room layout on a grid.
Graphviz Quick and Dirty Rendering
It is of course possible to feed almost any graph to dot and get a reasonable visualization out of it.
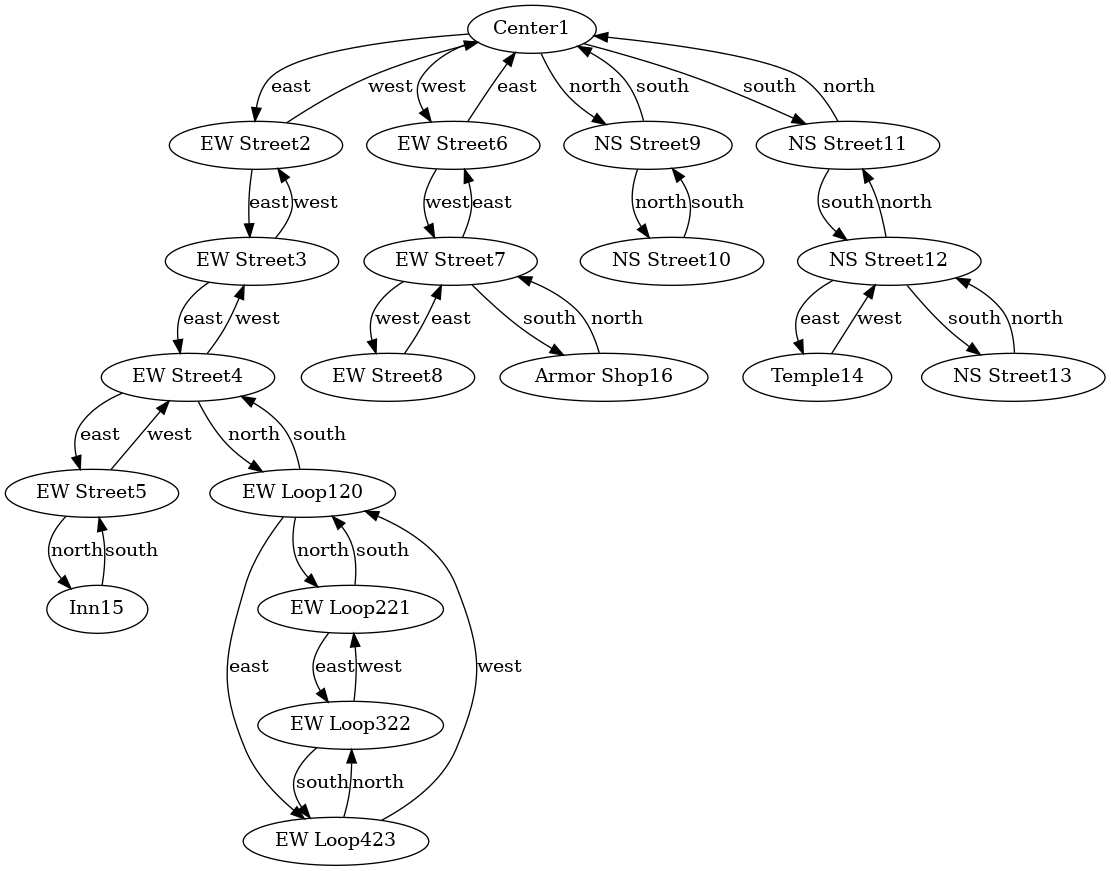
However, given our cardinal directions it would be nice to lay things out a little more sensibly on a cartesian coordinate grid. It turns out to be relatively simple and possible in linear time. One loop iteration for each room along with a bit of memory to keep track of parent/child relationships.
________________________________ 0: [ ] [ ]-[ ] | 1: | | | | 2: [ ] [ ]-[ ] | 3: | | | | 4:[ ]-[ ]-[ ]-[+]-[ ]-[ ]-[ ]-[ ] | 5: | | | 6: [ ] [ ] | 7: | | 8: [ ]-[ ] | 9: | | 10: [ ] | 11: |
That would be neat and enable something like a "map" command so players could more easily figure out where they are at and what nearby rooms there are. Let's take a quick look at the data structure that a typical MUD might have. These structures are simplified for illustrative purposes:
type exit struct { dir string from *room to *room } type room struct { id uint64 short string // short description of room long string // long description exits map[string]exit }
Example continue:
func main() { rooms := []room{ room{0, "center", "center long", make(map[string]exit)}, room{1, "street e", "a street long", make(map[string]exit)}, room{2, "street e", "a street long", make(map[string]exit)}, room{3, "street e", "a street long", make(map[string]exit)}, room{4, "armor shop", "armor shop long", make(map[string]exit)}, room{5, "street w", "a street long", make(map[string]exit)}, } // Connect some rooms like below: // [4] // | // [5]-[0]-[1]-[2]-[3] connect(&rooms[0], &rooms[1], "east") connect(&rooms[1], &rooms[0], "west") connect(&rooms[0], &rooms[5], "west") connect(&rooms[5], &rooms[0], "east") connect(&rooms[1], &rooms[2], "east") connect(&rooms[2], &rooms[1], "west") connect(&rooms[2], &rooms[3], "east") connect(&rooms[3], &rooms[2], "west") connect(&rooms[3], &rooms[4], "north") connect(&rooms[4], &rooms[3], "south") bfs(&rooms[0]) }
And the traversal function, using Breadth First Search:
func bfs(r *room) { queue := []*room{r} visited := make(map[uint64]bool) for len(queue) > 0 { lsize := len(queue) for lsize != 0 { lsize-- current := queue[0] queue = queue[1:] visited[current.id] = true fmt.Println("room: ", current) for _, e := range current.exits { if _, seen := visited[e.to.id]; !seen { queue = append(queue, e.to) } } } } }
This variant of BFS processes each level all at once, although that is not relevant here. BFS efficiently traverses this graph. A complicating factor for MUDs is that their graphs include cycles, so the visited map keeps track of rooms it has already visited. With some small tweaks to BFS we can lay everything out on a coordinate system. My approach is to treat whatever room traversal starts from as the origin. Anything to the west on the x axis is negative and east is positive. Anything north on the y axis from origin is positive and anything south is negative. With this idea in mind let's modify our bfs function to track coordinates as we traverse.
Change things up and track coordinates the function performs traversal:
func bfs(r *room) []string { queue := []*room{r} visited := make(map[uint64]bool) traveled := make(map[*room]parent) traveled[r] = parent{r, 0, 0} for len(queue) > 0 { lsize := len(queue) for lsize != 0 { lsize-- current := queue[0] queue = queue[1:] visited[current.id] = true for dir, e := range current.exits { if _, seen := visited[e.to.id]; !seen { x, y := coord(dir, traveled[current].x, traveled[current].y) traveled[e.to] = parent{current, x, y} queue = append(queue, e.to) } } } } result := make([]string, 0) for k, v := range traveled { // fmt.Printf("dir: %s --> [%d,%d]\n", k.short, v.x, v.y) result = append(result, fmt.Sprintf("room: %s, coords: [%d,%d]\n", k.short, v.x, v.y)) } return result }
There are couple more supporting elements now:
// This also tracks a room's coordinates and its parent (from). type parent struct { from *room x int y int } func coord(dir string, x int, y int) (int, int) { switch dir { case "north": y += 1 case "south": y -= 1 case "west": x -= 1 case "east": x += 1 } return x, y }
The central observation is that as each element is queued up the function has all the facts it needs to figure out each element being enqueued's coordinates. The current node is known via the traveled map and the enqueued node's direction is known. The traveled map keeps track of how things were traversed and preserves state data. In recursive implementations of graph traversal this information can be passed on the stack, here we use a convenient map. Saving the to-be-visited node, along with its parent and the new x and y coordinates will provide the coordinates for every node in the graph!
room: street e, coords: [2,0] room: street e, coords: [3,0] room: armor shop, coords: [3,1] room: center, coords: [0,0] room: street e, coords: [1,0] room: street w, coords: [-1,0]
These coordinates can then be used for a variety of layout purposes to visualize the rooms. It is easily possibly to connect rooms in a way that they overlap. Up and down are also common directions, but those don't make sense on a single grid. It is also easy to keep track of conflicting coordinates and display those. Pretty helpful! Although this looks simple, it took a bit of thinking, so I thought I would share.
